UNIDAD IV: DERIVADAS

Responsables: Todos los estudiantes

Objetivos Específicos:

1) Interpretar el concepto de derivada de una función en un punto función Analítica y gráficamente.

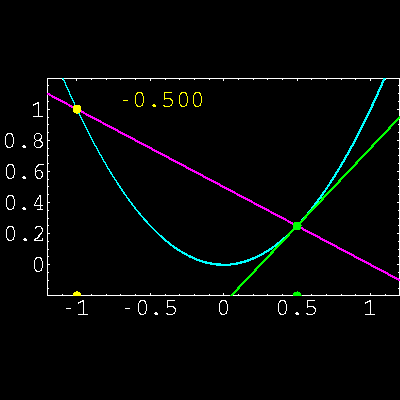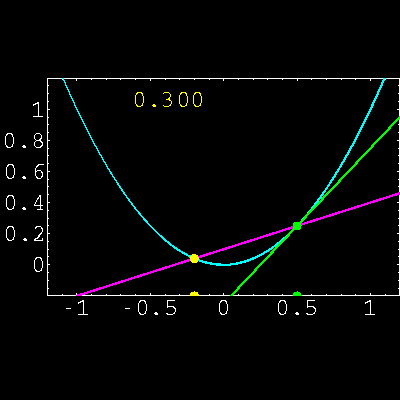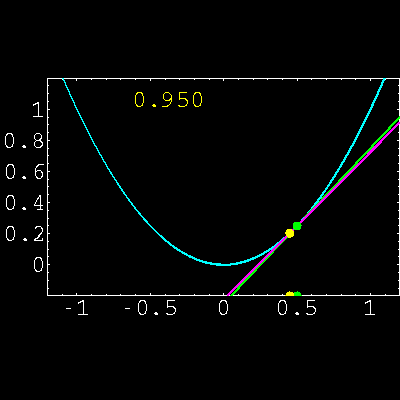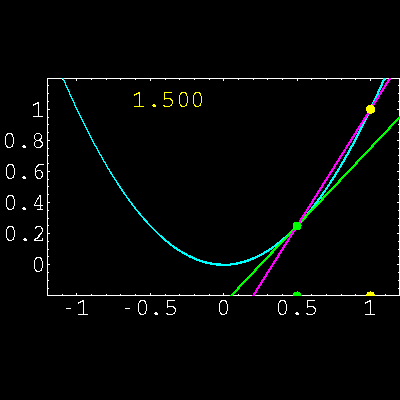
2) Aproximar funciones utilizando la fórmula de Taylor, interpretando el significado real de la fórmula.

3) Aplícar los conceptos de derivabilidad de funciones en la demostración de problemas.

Contenidos:

1) Derivada de una función en un punto

• Definición, interpretación geométrica y física. Existencia de la derivada.
• Derivadas laterales.

2) Función derivable.

3) Reglas de la derivación.

• Derivada de una constante.
• Derivada de la función identidad.
• Derivada de una constante por una función
• Derivada de función de función.
• Derivada de la función inversa.
• Derivada de la suma, producto y cociente de funciones.
• Derivada de funciones elementales.
• Derivada de la función potencial.
• Derivada de funciones circulares directas e inversas.
• Derivada de la función logarítmica y exponencial.
• Derivadas sucesivas.
• Derivada de la función implícita

4) Signo de la derivada. Máximos mínimos y relativos. Puntos de inflexión.

5) Métodos de las derivadas sucesivas. Concavidad y convexidad.

6) Teorema de Rolle. Teorema de Lagrange. Teorema de Cauchi. Límites del cociente de dos infinitésimos.

7) Regla de L'Hopital.