GUÍA DE SERIES Y SUCESIONES

SERIES Y SUCESIONES

Omaira Ordaz -Series y Sucesiones

María José Martínez -Series Geométricas y Armónicas

UNIDAD III: LÍMITES Y CONTINUIDAD

1) Límites de funciones reales de una variable real

• Definición de límite de una función. 

• Unicidad del límite. Límite por sucesiones

• Límites infinitos y límites en el infinito

• Cálculo de límites

• Límites laterales

• Límites de funciones elementales

• Límites y desigualdades

• Condición de Cauchy para funciones

• Límites de restricciones y extensiones de funciones

2) Funciones continuas
Definiciones de continuidad. Operaciones con funciones continuas

 





 Guia de Ejercicios

 

En desarrollo...

Series y Sucesiones

PLAN DE EVALUACIÓN

FUNDAMENTACIÓN

El análisis es una rama de la matemática que estudia los números reales, los complejos, los vectores y sus funciones. Se empieza a desarrollar a partir del inicio de la formulación rigurosa del cálculo y estudia conceptos como la continuidad, la integración y la diferenciación de diversas formas.

El Análisis matemático de una variable real, conjuntamente con el Álgebra, son los pilares básicos para el estudio de la Matemática pura y aplicada. El núcleo esencial es el cálculo diferencial e integral, y en torno a este núcleo se van configurando otros elementos que le dan consistencia y fundamento o que sirven para ilustrar la enorme utilidad, para una gran variedad de problemas, de los conceptos y técnicas desarrollados en el curso. 

La asignatura profundiza, fundamenta y completa conocimientos que se poseen sobre esta materia y sirve de cimiento e instrumento para el estudio de otros temas más avanzados del Análisis Matemático que se abordan en cursos posteriores. 

El Cálculo Diferencial e Integral es uno de los pilares fundamentales de la Matemática, y como tal es de vital importancia por sus aplicaciones prácticas a diversas disciplinas, entre las que se halla principalmente la Física. En el caso particular de la asignatura Análisis Matemático, se estará estudiando el caso más general de las funciones de varias variables reales. Además se estudiarán las ecuaciones diferenciales ordinarias y a través de ellas, diversas aplicaciones al modelado matemático. 

Todo esto permitirá al participante tener una visión global del Análisis, lo cual le permitirá relacionar contenidos para lograr así una mejor fijación y posteriormente aplicar los conocimientos adquiridos a problemas diversos de la vida real. Este curso es de carácter teórico-práctico ya que enfatiza el desarrollo, dominio y aplicación de saberes y haceres (teórico-prácticos) así como la adquisición de habilidades y destrezas cognitivas y motoras, bajo la dirección, asesoría y supervisión del facilitador, que puede o no requerir de ambientes e instrumentos especiales, independientemente de la modalidad de administración e implementación metodológica de ellos.

UNIDAD I. CONJUNTO DE LOS NÚMEROS REALES

Responsables:  Virginia Salazar, Moises Ramos y Francisco Marcano 

 

OBJETIVOS ESPECÍFICOS:

Fundamentar el conjunto de los números reales y las propiedades de las aplicaciones entre números reales, así como la definición de las funciones elementales.

Aplicar las propiedades del sistema de los números reales en la solución de problemas cuyo planteamiento, análisis y discusión requieran el uso de dichas propiedades o de sus consecuencias.

Interpretar las nociones básicas de la topología de espacios métricos como elementos fundamentales sobre los cuales se basa el estudio del análisis matemático.

 

CONTENIDOS:

 1) Sistemas numéricos

• Números naturales: principio de inducción

• Números enteros y racionales

• Números reales: operaciones algebraicas

2) Sistema de números reales

• Conjunto ordenados

• Campos. Propiedades

• Campo real. Propiedades

3) Coordinabilidad entre conjuntos

• Conjunto coordinables. Propiedades

• Conjuntos finitos e infinitos. Propiedades

• Conjuntos numerables y no numerables. Propiedades

4) Topología de espacios métricos

• Definiciones básicas. Propiedades

• Conjuntos compactos. Propiedades

• Conjuntos conexos. Propiedades

UNIDAD II: SUCESIONES

Responsables: Crisenys Lárez, Omaira Ordaz, María J. Martínez

Objetivos Específicos:

• Interpretar los conceptos de sucesiones y series convergentes.
• Aplicar el teorema de Cauchy en las demostraciones de sucesiones y series.

Contenidos:

1) Sucesiones convergentes

• Definición de sucesión.
• Sucesiones acotadas y sucesiones convergentes.
• Límite de una sucesión convergente
• Sucesiones monótonas
• Operaciones con sucesiones

2) Sucesiones de Cauchy.

• Límite superior e inferior de una sucesión

3) Series numéricas

• Definición y primeras propiedades
• Series: términos y sumas parciales. Series convergentes, divergentes y oscilantes
• Linealidad de la convergencia de series
• Condición necesaria para la convergencia de una serie. Condición general de convergencia de Cauchy
• Series de términos no negativos. Convergencia de una serie de términos no negativos.Criterios de comparación
• Propiedad conmutativa para series

UNIDAD III: LÍMITES Y CONTINUIDAD

Responsables:  Jarvelys Malavé, Marcel Ruíz, Paulimar Alfonzo, Miguel Hernández

Objetivos Específicos:

• Interpretar los conceptos de límite y continuidad.
• Aplícar los conceptos de límite y continuidad en la demostración de problemas

Contenidos:

1) Límites de funciones reales de una variable real

• Definición de límite de una función. Unicidad del límite. Límite por sucesiones
• Límites infinitos y límites en el infinito
• Cálculo de límites
• Límites laterales
• Límites de funciones elementales
• Límites y desigualdades
• Condición de Cauchy para funciones
• Límites de restricciones y extensiones de funciones

2) Funciones continuas

• Definiciones de continuidad. Operaciones con funciones continuas
• Propiedades de las funciones continuas: teoremas de Weierstrass, Bolzano y Darboux; funciones continuas monótonas
• Clasificación de discontinuidades
• Continuidad uniforme. Teorema de Heine. Extensión de funciones continuas

UNIDAD IV: DERIVADAS

Responsables: Todos los estudiantes

Objetivos Específicos:

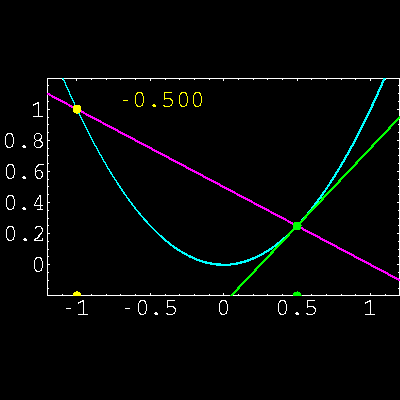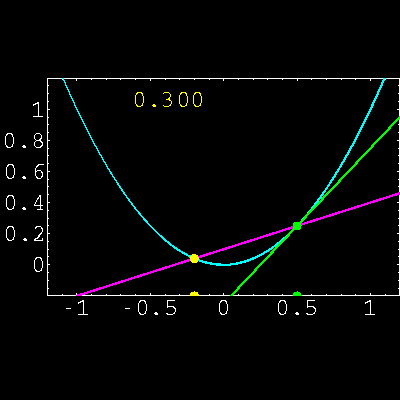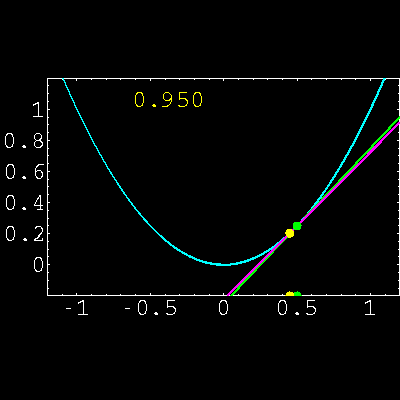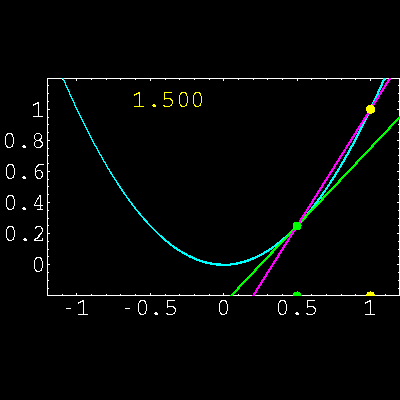
1) Interpretar el concepto de derivada de una función en un punto función Analítica y gráficamente.

2) Aproximar funciones utilizando la fórmula de Taylor, interpretando el significado real de la fórmula.

3) Aplícar los conceptos de derivabilidad de funciones en la demostración de problemas.

Contenidos:

1) Derivada de una función en un punto

• Definición, interpretación geométrica y física. Existencia de la derivada.
• Derivadas laterales.

2) Función derivable.

3) Reglas de la derivación.

• Derivada de una constante.
• Derivada de la función identidad.
• Derivada de una constante por una función
• Derivada de función de función.
• Derivada de la función inversa.
• Derivada de la suma, producto y cociente de funciones.
• Derivada de funciones elementales.
• Derivada de la función potencial.
• Derivada de funciones circulares directas e inversas.
• Derivada de la función logarítmica y exponencial.
• Derivadas sucesivas.
• Derivada de la función implícita

4) Signo de la derivada. Máximos mínimos y relativos. Puntos de inflexión.

5) Métodos de las derivadas sucesivas. Concavidad y convexidad.

6) Teorema de Rolle. Teorema de Lagrange. Teorema de Cauchi. Límites del cociente de dos infinitésimos.

7) Regla de L'Hopital.

Bibliografía sugerida

• Apostol, T.M.(1999). Calculus, Vol I. Reverté, Barcelona
• Bartle, R. G. y Sherbert, D. R.(1990). Introducción al Análisis Matemático de una variable. Editorial Limusa, México
• Fuertes, J. y Martínez, J.(1997). Problemas de Cálculo Infinitesimal. Col. Schaum. McGraw-Hill, Madrid
• Ortega, J. M.(1995). Introducción al Análisis Matemático. Editorial Labor